1、已知三角形ABC中,AC=3,BC=4,AB=5,P是三角形ABC内一点,求PA+PB+PC的最小值.
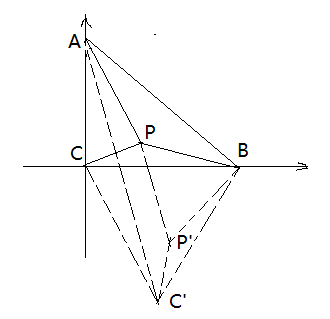
解:由题意三角形ABC为直角三角形,以直角顶点C为原点,CB为x轴,CA为y轴建立坐标系(如图)
则C(0,0)A(0,3)B(4,0)
以B为旋转中心,将△BPC绕点B逆时钟旋转60°至△BP'C',连接PP'、CC'、AC'
则△BPP',△BCC'均为等边三角形
所以PB=PP',PC=P'C'
所以PA+PB+PC=AP+PP'+P'C'≥AC'
而C'(2,-2√3)
所以AC'=√[(0-2)?+(3+2√3)?]=√(25+12√3).
即PA+PB+PC的最小值等于AC'的长√(25+12√3).
2、已知三角形ABC中,AB=10,AC=17,BC=21,P是三角形ABC内一点,求PA+PB+PC的最小值.
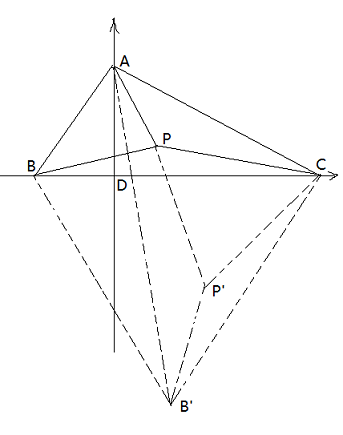
由勾股定理得AD?=10?-x?=17?-(21-x)?,解得x=6,AD=8,DC=15
以D为坐标原点,BC为x轴,DA为y轴建立坐标系(如图)
则A(0,8)B(-6,0)C(15,0)
以C为旋转中心,将△CPB绕点C逆时钟旋转60°至△CP'B',连接PP'、BB'、AB'
则△CPP',△CBB'均为等边三角形
所以PC=PP',PB=P'B'
所以PA+PB+PC=AP+PP'+P'B'≥AB'
而B'(9/2,-21√3/2)
所以AB'=√[(0-9/2)?+(8+21√3/2)?]=√(415+168√3).
即PA+PB+PC的最小值等于AB'的长√(415+168√3).
【 补充说明】如图,以△ABC的三边为边,分别向外作等边三角形BCD、ACE、ABF,连接AD、BE、CF,则(1)AD、BE、CF交于一点P,且∠APB=∠APC=∠BPC=120°,(2)P到A、B、C三顶点距离的和最小,且PA+PB+PC=AD=BE=CF。
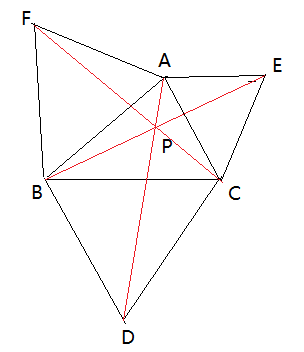
证明:∵AF=AB,∠FAC=∠BAE,AC=AE
∴△AFC≌ABE
∴CF=BE
同理可证△BCF≌BDA,CF=AD
∴AD=BE=CF.
∵△AFC≌ABE
∴∠AFC=∠ABE
∴∠BPF=∠BAF=60°,∠BPC=120°
同理可证∠APB=∠APC=120°
∴∠APB=∠APC=∠BPC=120°
至于P到三顶点距离之和为何最小上面两题已明。